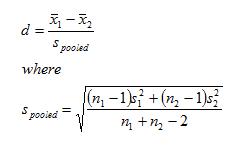71 голосов
IgG к SARS-CoV-2
почему?
Какая разница 100 человек взяли в одно исследование или те же 100 человек по 10 человек в 10 исследований?
почему то что дает лучшие прогресс за 08:12 недель не даст лучше прогресс за год?
Ты видел там прибавки? Умножь их на 8 и года на три. Всех бы порвало нах
Старожил
те же 100 человек по 10 человек в 10 исследований?
Исследования могут сильно разниться по качеству в силу различных причин... следовательно тут уже 10х10 не равно 100!
Аксакал
поэтому и лучше 10 по 10Исследования могут сильно разниться по качеству в силу различных причин... следовательно тут уже 10х10 не равно 100!
IgG к SARS-CoV-2
и что это значит?
это значит, что краткосрочные результаты ниочем. их нельзя в уме продолжать на 10 лет от дрыща до чемпиона Олимпии
Сообщение изменено: oscid (06 декабря 2024 - 04:56)
Невыступающий неспортсмен
почему если в 10: исследование буду сравнивать одни и те же параметры
Так у них обычно дизайн различный. То в одном бабушки, то в другом спортсмены, то протоколы разные сравниваются, то паузы отдыха отличаются и т.д...
Старожил
почему если в 10: исследование буду сравнивать одни и те же параметры
Евгений, даже в твоей ссылке чёрным по белому написано:
<<Как видите, мощность выборки очень низкая, если в каждой группе по 10 участников (что является стандартом в фитнес-исследованиях), и для достижения статистической значимости нам необходимо выявить очень большие различия эффектов (различия между группами). Если следовать общепринятой практике и стремиться к мощности выборки в 80% (0,8), то нам нужны большие эффекты или большие размеры выборки. В исследованиях по фитнесу эффекты обычно небольшие, как и размеры выборки. Следовательно, исследования вряд ли обнаружат разницу между группами, даже если она существует.>>
Злостный ПРОВОКАТОР!
Нафига?Тебе мои дрищевские штанги разве что по полу катать, Санёк
Пусть женщины такое пополу катают.
Результат-то твой хде? Мышцов-то и нетути... и не будет.
Зато весу больше моего! Хотя да... для этого и тренироватсо собственно не нужно...
Ну ничего... зато медаль и грамота!
Я так понял, что аргументов от тебя так и не будет.
Злостный ПРОВОКАТОР!
Это не принципиально...там непонятно новички или стажные
Тем не менее после периода тренировки СМП становится более чувствительным к специфическому типу упражнений, вызывая синтез отдельных субклеточных белковых фракций (митохондриальной или миофибриллярной), впоследствии проявляясь в фенотипических изменениях, характерных для разных видов тренировки
Новичков дольше синтез продолжается
С точностью до наоборот! Они быстрее и резче реагируют, но синтез продолжается меньше просто потому, что для более длительных эффектов нужна заметно выше тренированность и интенсивность нагрузки.
Аксакал
Новичок
Лучше обобщëнный вывод.)Exercise-induced increases in MPS are shorter lived and peak earlier in the trained state than in the untrained state, resulting in a smaller overall muscle protein synthetic response in the trained state
https://pubmed.ncbi....h.gov/25739559/
Перевести или так сойдёт?
Невыступающий неспортсмен
Лучше резюмировать, а то не понял нифига )Exercise-induced increases in MPS are shorter lived and peak earlier in the trained state than in the untrained state, resulting in a smaller overall muscle protein synthetic response in the trained state
https://pubmed.ncbi....h.gov/25739559/
Перевести или так сойдёт?
Аксакал
Злостный ПРОВОКАТОР!
Результаты показывают, что величина синтеза миофибриллярных белков зависит от интенсивности, увеличиваясь от 20 %, и достигает плато между 60 и 90 % РМ. Требуются дополнительные исследования для выяснения влияния объема работы и адаптивного ответа обмена мышечного белка при различной интенсивности нагрузки.
Ключевое выделил.
для более длительных эффектов нужна заметно выше тренированность и интенсивность нагрузки.
А при правильном построении программы, даже если бы синтез продолжался только 48 часов, что само по себе абсурд, то даже тренировки МГ один раз в недели при 3-хразовом бросплите обеспечивают ПОСТОЯННЫЙ повышеный синтез белка и даже базовый.
Несколько работ отметили, что тренировка с отягощением увеличивает базальный уровень СМП (5, 86). Также было показано, что даже кратковременная (2 недели) тренировка с отягощениями увеличивает СМП в покое,
Аксакал
или размер эффектов был бы просто неприлично значимым
Кстати, кто-то понимает, в чем адский смысл вычисления размера эффекта, как частного от среднего прироста, деленного на разброс исходных или конечных результатов? Понятно было бы, если бы делили на разброс приростов. Надо у Длора спросить.
Новичок
в чем адский смысл вычисления размера эффекта
Адского смысла нет. Просто стандартизированная метрика количественной оценки различий с учётом масштаба и вариабельности.
Где-то измеряют в килограммах, где-то в километрах. А размер эффекта различий позволяет привести к общепринятому масштабу и оценивать, насколько сильны различия. Создать более-менее универсальную шкалу, что Коэн в свое время и сделал.
Если вариабельность выше (распределения сравниваемых групп сильнее перекрываются), то размер эффекта будет ниже.
И то, и другое достигается делением на стандартное отклонение.
Кстати, для связанных групп там немного иначе размер эффекта вычисляется, в знаменателе иначе
Сообщение изменено: Dlor (07 декабря 2024 - 12:34)
Заслуженный ветеран
Адского смысла нет. Просто стандартизированная метрика количественной оценки различий с учётом масштаба и вариабельности.
Где-то измеряют в килограммах, где-то в километрах. А размер эффекта различий позволяет привести к общепринятому масштабу и оценивать, насколько сильны различия. Создать более-менее универсальную шкалу, что Коэн в свое время и сделал.
Если вариабельность выше (распределения сравниваемых групп сильнее перекрываются), то размер эффекта будет ниже.
И то, и другое достигается делением на стандартное отклонение.
Кстати, для связанных групп там немного иначе размер эффекта вычисляется, в знаменателе иначе
Понятно одно. Надо будет ебашить и прибавлять по возможности.
The Experience Machine
Понятно было бы, если бы делили на разброс приростов.
Его же объединять для двух групп нельзя. Бессмыслица получится. А стандартное отклонение — можно и нужно. Точнее, разбросы приростов тоже можно использовать (без объединения), но только в тех случаях, когда у нас одна группа до опыта (воздействия фактора, эффект которого измеряем), а вторая после. То есть, без контрольной группы.
Аксакал
Адского смысла нет. Просто стандартизированная метрика количественной оценки различий с учётом масштаба и вариабельности.
Где-то измеряют в килограммах, где-то в километрах. А размер эффекта различий позволяет привести к общепринятому масштабу и оценивать, насколько сильны различия. Создать более-менее универсальную шкалу, что Коэн в свое время и сделал.
Если вариабельность выше (распределения сравниваемых групп сильнее перекрываются), то размер эффекта будет ниже.
И то, и другое достигается делением на стандартное отклонение.
Кстати, для связанных групп там немного иначе размер эффекта вычисляется, в знаменателе иначе
А почему бы не делить на стандартное отклонение самой прибавки? Это было бы логичнее. Типа если прибавили 10 кг плюс минус 1 кг, то размер эффекта выше, чем прибавили 10 кг плюс минус 20 кг. А так выходит, что прибавку 10 кг делят на стандартное отклонение в исходных результатах. Как-то не ясно, чем это лучше, чем просто сравнивать средние прибавки.
Хотя, как я понял, на стандартное отклонение прибавок делят, когда p считают.
Новичок
А почему бы не делить на стандартное отклонение самой прибавки? Это было бы логичнее. Типа если прибавили 10 кг плюс минус 1 кг, то размер эффекта выше, чем прибавили 10 кг плюс минус 20 кг. А так выходит, что прибавку 10 кг делят на стандартное отклонение в исходных результатах. Как-то не ясно, чем это лучше, чем просто сравнивать средние прибавки.
Хотя, как я понял, на стандартное отклонение прибавок делят, когда p считают.
Так, еще раз перечитал свое прошлое сообщение с ответом. Надо внести некоторые уточнения, так как нефиг писать поздно ночью с температурой под 38.
Для связанных групп ты прав, стандартное отклонение прибавок информативнее. И для связанных групп именно оно идет в знаменателе.
Попробую пояснить для широкого круга читателей.
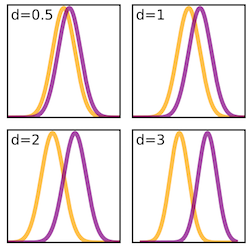
Размер эффекта позволяет ответить на вопрос, насколько сильно отличаются два распределения интересующих нас признаков. Если эти распределения полностью перекрываются, то размер эффекта равен 0. Чем дальше друг от друга и чем меньше перекрытие, тем больше величина эффекта.
При условии, что распределение близко к нормальному (гауссову), на меру этого перекрытия будут влиять среднее значение (вокруг него плотнее группируются остальные наблюдения) и стандартное отклонение (как мера вариации, насколько плотно вокруг среднего "уложены" другие наблюдения). Они и берутся в расчет.
Самый распространенный размер эффекта для сравнения двух групп - d Коэна.
Но! Есть вариант для несвязанных групп, а есть для связанных.
Несвязанные - это разные группы наблюдения по одним и тем же признакам. Например, изучаем плотность костей в группе 20-30-летних и группе 65+. Это разные люди.
Там считается так:
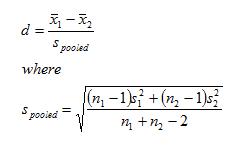
То есть разность средних сравниваемых групп, деленное на хитрое обобщенное стандартное отклонение, вычисленное на основе параметров сравниваемых групп.
Связанные группы. Частный случай - повторные измерения после воздействия, как в исследованиях.
Взяли группу, измерили до, измерили после, сравнили. Люди те же, для каждого есть показатель до и после.
В этом случае размер эффекта вычисляется на основе среднего разностей до-после по каждому наблюдению, деленного на стандартное отклонение этих разностей.
Кроме того, его можно также вычислить на основе t-статистики для связанных групп, коэффициента корреляции между до-после, но это все вариации, дающие в итоге одну и ту же оценку.
Ну и куча дополнительных вариантов этих размеров эффекта для оценки нескольких групп, с коррекциями на несбалансированность и т.п. Но чаще всего публикуют или d Коэна, или g Хэджеса (модификация для предыдущего, когда размеры групп не равны).
Кратенько вот тут можно почитать: https://www.datanovi...hens-d-measure/
Сообщение изменено: Dlor (07 декабря 2024 - 01:38)
Завсегдатай
а спина за эти годы выросла? Она у тебч отсутствовала всегда. Интересно как методика справляется когда генетики нетВидимо именно поэтому руки за эти годы выросли меньше всего.
Аксакал
В этом случае размер эффекта вычисляется на основе среднего разностей до-после по каждому наблюдению, деленного на стандартное отклонение этих разностей.
Ну да. Так логично. Но вроде в этих статьях, когда описывают размер эффекта, делят на sd не разностей, а начальных результатов. Надо будет поискать по статьям, но вроде именно так делают.
Новичок
Но вроде в этих статьях, когда описывают размер эффекта, делят на sd не разностей, а начальных результатов. Надо будет поискать по статьям, но вроде именно так делают.
Странно... Если найдете и не затруднит, могли бы в тему эту скинуть ссылки или в личку.
Злостный ПРОВОКАТОР!
Естественно... И в ширину и толщину и визуально... коллажи выкладывал на форуме и не раз.а спина за эти годы выросла?
Медленно, но уверенно!Интересно как методика справляется когда генетики нет
Аксакал
Странно... Если найдете и не затруднит, могли бы в тему эту скинуть ссылки или в личку.
Ну вот в одной из статей Шонфилд сослался на Морриса, как я понял, формулу (8).
https://sci-hub.ru/1...094428106291059
2 пользователей, 3 гостей, 1 скрытых
Вход
Регистрация
Наверх
